La conjetura de Collatz es un interesante enigma matemático que ha desafiado cualquier solución durante décadas y que esconde asombrosos patrones fractales con implicaciones dialécticas entre comportamientos azarosos y deterministas. El comportamiento de estos números tiene vinculación con la teoría del caos -que estudia la vinculación entre el orden y fenómenos aparentemente aleatorios- y otra teoría de la física, la teoría ergódica, que estudia el comportamiento promedio de fenómenos dinámicos que inicialmente parecen tener un comportamiento aleatorio pero terminan, a largo plazo, en un comportamiento previamente experimentado y determinado.
El problema consiste en elegir cualquier número natural y aplicar de forma reiterada la siguiente operación: “si se toma un número par, este es dividido entre dos; si el número es impar, este es multiplicado por tres y se le agrega 1 al resultado. Este proceso se realiza, de forma iterada, con los números obtenidos tras cada paso” .La conjetura establece que sin importar el número natural por el que se comience el resultado final será siempre 1. “De hecho, tras llegar a 1 este al iterarlo se convierte en 4, luego a 2 y nuevamente llegará a 1, estableciéndose un bucle” 4,2,1 se repite en un circuito infinito.
Por ejemplo, empezando por 9, encontramos como resultado de las iteraciones la siguiente serie: 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. “La conjetura de Collatz presenta un comportamiento caótico, no es posible determinar si la cantidad de pasos necesarios para que el número llegue a 1 obedece a si el número es grande o pequeño” . Vimos que para el número 9 se requieren 19 iteraciones para llegar al 1 y comenzar el bucle infinito; para el 27 se requieren 111 pasos, mientras que para el 8192 se requieren apenas 13 iteraciones. O sea que la conjetura de Collatz combina los siguientes elementos: la aleatoriedad en el comportamiento de los primeros números que aparecen en las iteraciones, la determinación absoluta que implica que todos terminan en 1, y la existencia de un círculo infinito de 4,2,1 si seguimos la iteración a partir del final; aleatoriedad, determinación y un ciclo cerrado.
La Conjetura de Collatz es un problema que cualquier persona con conocimientos elementales de aritmética puede entender, pero que, en contraste con su prístina sencillez, no es claro si existe demostración posible o no. Fue compuesto por el matemático alemán Lothar Collatz en 1932 y circuló por primera vez entre sus colegas en 1950. Asombroso que a más de cinco décadas de ser enunciada, no pueda demostrarse la conjetura de una simple operación aritmética.
Se trata de “una conjetura, una de esas pesadillas que atormenta el entendimiento de los matemáticos, que perturba la conciencia y no permite dormir” . “¿Por qué se trata de un problema tan difícil a pesar de que es muy fácil de enunciar? […] Por un lado, los iterados tienen un comportamiento «pseudoaleatorio», es decir, aunque estén perfectamente definidos, parecen comportarse aleatoriamente”. En el 2020 las supercomputadoras demostraron que la conjetura es válida para todas las secuencias de números menores a 2 elevado a la 68 -hablamos de más de 295 trillones-. Un número increíblemente grande pero que está lejos de ser una demostración para la cantidad infinita de números naturales.
En los pasillos de las universidades se decía que dicho problema no era más que un complot urdido por los soviéticos para entretener a los matemáticos americanos en tareas inútiles. el matemático Alex Kontorovich afirmó que «entre los matemáticos profesionales, la conjetura de Collatz no es famosa, sino infame. Si alguien admite en público que está trabajando en ella, eso significa que algo malo pasa con ese matemático». Por su parte, el matemático Paul Erdös afirmó al respecto: «las matemáticas, a día de hoy, no están lo suficientemente maduras para tales preguntas». El desafío es tal que existe un premio de 1.085.000 dólares- el monto más alto por un problema matemático no resuelto- a quien logre alguna demostración.
Pero grandes revoluciones en el pensamiento científico han partido de “excentricidades” que contradecían el “sentido común” dominante, de aparentes “monstruosidades” que desafiaban los dogmas establecidos. Los números irracionales -por ejemplo- trastornaron la mente cerrada de los viejos pitagóricos quienes intentaron ocultar su existencia, las estructuras fractales parecían meras curiosidades hasta mostrarse como una forma fundamental de la naturaleza -mucho más presentes que las rígidas figuras geométricas euclideanas- y hasta el descubrimiento de que el espacio se dobla de partió del estudio de la órbita excéntrica de mercurio.
No necesariamente la conjetura de Collatz contiene el germen de descubrimientos revolucionarios como esos. Por el momento los “números granizo” -que resultan de la conjetura, como veremos más adelante- se utilizan en programas para generar música y en el desarrollo de software que profundizan en patrones estadísticos, mismos programas que tienen el potencial de utilizarse en otros campos. Collatz mismo era un defensor de que las matemáticas deben aplicarse al mundo real. Pero por más que para muchos este problema sea sinónimo de una tarea inútil y sin objetivo alguno, esconde patrones muy interesantes que demuestran orden debajo del caos y la aleatoriedad. Al menos desde un punto de vista filosófico muestran la vinculación entre el azar y la necesidad, de patrones que se ocultan debajo de la superficie, incluso de patrones fractales de una infinita complejidad. Si bien hasta el momento no se ha podido encontrar ningún patrón que resuelva si es verdadera o no.
Bucles de diferente tipo y el infinito
La conjetura implica, de cierta manera, la unidad entre lo aleatorio y la determinación más cerrada y absoluta. Pero podría objetarse que a pesar de su aleatoriedad, finalmente el proceso termina en un bucle cerrado. Un bucle es lo contrario a un movimiento dialéctico que implica un proceso abierto y progresivo, una espiral. Más bien estaríamos ante un ejemplo del “eterno retorno de lo mismo”, una imagen estoica que impresionó poéticamente a Nietzsche. Pero la dialéctica es siempre concreta y se manifiesta de manera determinada en cada nivel de la realidad y través de un proceso contradictorio en sí mismo. El pensamiento dialéctico no impone nada a los procesos, sino que, al contrario, éstos tienden a reforzar la idea de movimiento y desarrollo contradictorio, de forma en sí misma contradictoria. Para aterrizar esto veremos que nuevos patrones pueden emerger si cambiamos cuantitativamente la fórmula.
La conjetura sería parte integrante de una serie de fórmulas del mismo tipo que contienen comportamientos diferentes. Así, los bucles serían parte integrante de una serie de patrones más variados y complejos que los contienen, tanto como a series que se disparan al infinito. El comportamiento dialéctico es mucho más claro considerando al fenómeno desde una escala precisa. Por ejemplo: la conjetura 3n+1 termina siempre, o eso parece, en el ciclo 4,2,1. Pero si como “n” tomamos enteros negativos y aplicamos las mismas reglas (si es par lo dividimos entre 2 y si es impar aplicamos 3n+1), entonces se producen ciclos diferentes que termina y comienza siempre con el número con el que se inicia la operación. Ya no tenemos un movimiento aleatorio que termina en un bucle, sino directamente un bucle que comienza y termina por el mismo punto. Heráclito había señalado que “el principio y el fin de la circunferencia es el mismo”. Esto significa que un cambio cuantitativo puede generar un ciclo cualitativamente diferente. Por ejemplo con -17:
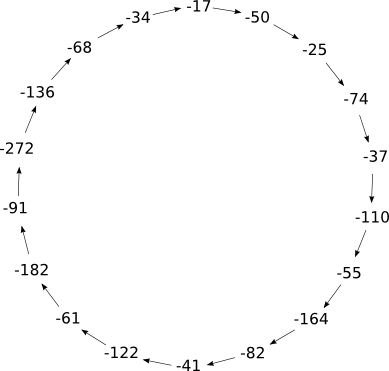
¿Pero ante este tipo de iteraciones con encontramos siempre ante bucles?. Parece que no siempre. Una fórmula del mismo tipo que la de Collatz pero ahora 5n+1 resulta, por ejemplo, para el número 1 en un ciclo de 5 números que comienza y termina por el 1 -o sea un círculo cerrado-, pero con el 7 los números se disparan aparentemente de forma indefinida, hasta el infinito. O por lo menos eso parece. Parece ser que estamos ante una trayectoria no acotada, que se dispara sin fin para ciertos números. Aunque tampoco existe manera de probar, hasta ahora, que para esos números que divergen y se disparan al infinito, no existe -a su vez- algún punto -por grande que sea- donde decaigan.
Con estos elementos se podría especular que la fórmula de Collatz forma parte de una serie formulas del mismo tipo, algunas de las cuales resultan en ciclos acotados: ya sea que comiencen por series aleatorias que terminan por decaer hasta un pequeño bucle, otras fórmulas que impliquen círculos desde un comienzo, o en fórmulas que incluyan números que se disparan sin fin. La diferencia entre esas fórmulas de una misma clase es simplemente cuantitativa, es decir, que esos pequeños cambios resultan en procesos cualitativamente distintos: bucles diferentes, unidos o no a series inicialmente aleatorias, y en procesos sin fin. Pero por ahora no hay manera de probar que en cada una de esas iteraciones no existan o no trayectorias divergentes.
Patrones y leyes subyacentes
Y parece ser que cada fórmula contiene, a su vez, patrones subyacentes. Por lo menos es así con la fórmula clásica 3n+1. Nos encontramos con nuevos patrones implícitos si consideramos a una gran cantidad de números y lo sometemos a la misma operación. Incluso dentro de un proceso que termina en un bucle cerrado, si observamos desde una perspectiva adecuada, los procesos dialécticos emergen.
Encontramos patrones en la forma en que los números rebotan en la gráfica antes de llegar al uno. Vimos, por ejemplo, que el número 27 rebota 111 veces antes de llegar al ciclo 4,2,1; el resultado más alto que alcanza en esas 111 veces es el 9232. Si fuera en metros hablaríamos de que el 27 parte de 27 metros para llegar más alto que el monte Everest. Al 26, en contraste, apenas le toma 10 pasos llegar al 1 y su altura máxima es de apenas 40. Por la forma en que los números rebotan rebotan antes de caer al suelo -como el granizo que rebota en una nube antes de caer de forma definitiva- son conocidos como “números granizo”. Resulta sorprendente que a partir de un comportamiento desordenado y caótico surja, en un momento dado, un comportamiento perfectamente predeterminado. Debido a este comportamiento se ha relacionado a la conjetura de Collatz con la teoría del caos, pues ésta estudia fenómenos en donde los cambios cuantitativos en un comportamiento caótico -como una tormenta tropical- generan estructuras organizadas -como un huracán- en un punto determinado. Vemos aquí una serie de puntos críticos en los cuales el comportamiento caótico de los números encuentra un pico (una cota), luego los números comienzan a decaer, hasta que -al parecer- indefectiblemente terminan en uno, o mejor dicho, en un pequeño bucle.
El comportamiento aleatorio de estos números es similar a la gráfica del mercado de valores, pues ambos movimientos son ejemplo del movimiento geométrico browniano, patrón que dibuja un fractal infinitamente quebrado, aunque en el primer caso lleve una tendencia descendente. Marx, por su parte, descubrió que debajo del comportamiento aleatorio y anárquico del mercado existen leyes deterministas que explican su comportamiento y crisis.
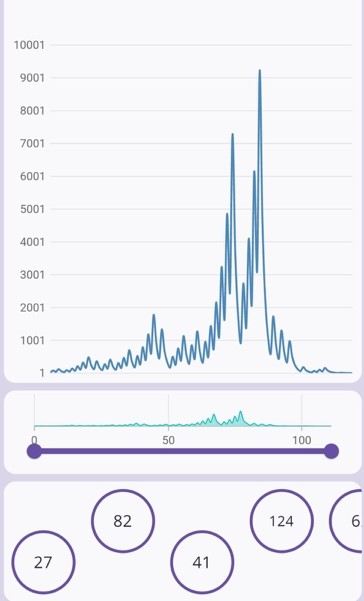
De hecho, a medida que obtenemos un mayor número de secuencias aparecen más patrones deterministas. Por ejemplo, aparecen regularidades estadísticas en la frecuencia en que aparecen, en el primer dígito de las secuencias de números en cada iteración, los números del 1 al 9. Resulta que si se representa la frecuencia de estos números en un histograma, para el primer millón de millones de secuencias aparece un patrón estable: el 30% de la secuencias comienzan con 1, el 17.5% comienzan por 2, el 13% con 3,etcétera; de acuerdo a la siguiente tabla:
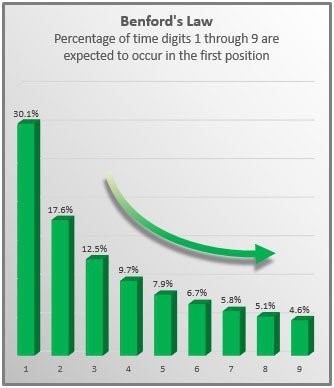
Este patrón de distribución obedece a la ley de Benford, y se utiliza para descubrir fraudes, pues si un comportamiento aparentemente aleatorio -por ejemplo el comportamiento de los votos de una elección- no obedece a esta ley, es muy probable que exista manipulación. Este patrón estadístico lo encontramos en gran cantidad de fenómenos: en la dinámica de las poblaciones, las cotizaciones de la bolsa, en las constantes físicas y en la sucesión de Fibonacci .La leyes de probabilidad se imponen de una forma particular a través de la aleatoriedad y el accidente. Ya decía Hegel que la necesidad hace uso del accidente, las leyes que rigen la realidad se manifiestan por una serie de casualidades.
Si graficamos para cada número natural -por ejemplo del 1 hasta el 9999- el número de iteraciones que requiere para decaer hasta el 1 obtenemos una imagen que tiende a mostrar un peculiar patrón entretejido:
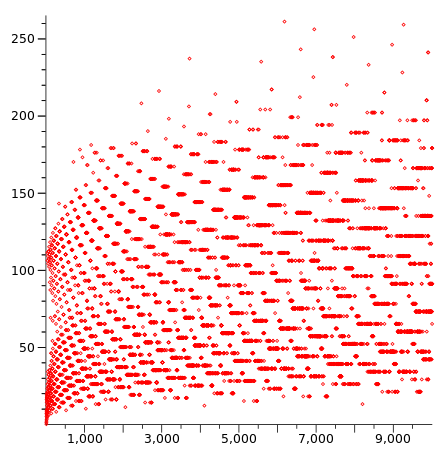
Mismo patrón que aumenta en densidad a medida en que se incrementan los números graficados, por ejemplo del 1 al 10 millones:
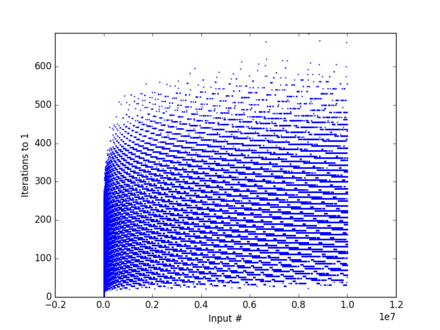
Fractales ocultos
Otro patrón interesante resulta si graficamos la forma en que diversos números naturales confluyen todos hacia el bucle 4,2,1; resulta esto en una gráfica de árbol direccionada. Hasta ahora no se ha encontrado ningún número que esté desconectado de ese gran árbol, es decir, ningún número natural que al aplicarle la operación de Collatz no termine en 1. Como vimos, las supercomputadoras han comprobado que la conjetura de Collatz es válida al menos para una cifra de más de 295 trillones.
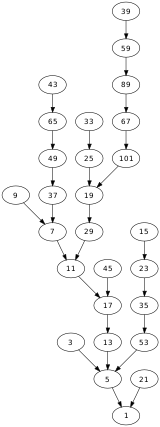

La direccionalidad que parecen tener los números naturales hacia el bucle 4,2,1 recuerda la atracción gravitacional que ejerce un agujero negro supermasivo a cuya fuerza ni siquiera la luz puede escapar “pues cualquiera sea el número del cual se parta, conduce siempre al mismo resultado, es decir, ningún número puede escapar del vórtice final de la sucesión de Collatz”. La gráfica direccionada de la que hemos hablado puede representarse en forma de vórtice (en la imagen vemos la representación de los números del 1 al 10 0009). ¿Existirá algún número superior al 2 elevado a la 68 que no confluya, ya sea porque -por alguna razón- se dispara al infinito o porque termina en un bucle diferente a 4,2,1? Hasta la fecha no se ha encontrado algún contraejemplo que refute la conjetura.

El matemático Terence Tao, de la universidad de California, es quien probablemente se ha acercado a la confirmación de la conjetura. Con estudios de probabilidad, publicados en el 2019, demostró que la conjetura es válida para “casi todo número”, aunque tampoco nadie ha encontrado nunca alguna excepción. O sea que la conjetura parece ser “casi cierta”. Tao escribe: “estamos ante una situación en donde parece haber una gran brecha entre «casi todos» y «todos» los resultados»” Aparentemente toda ley tiene sus excepciones pero no sabemos si la conjetura de Collatz es una excepción a la excepción, si existe algún número extraordinario que no confluya, alguna trayectoria excepcional, algún ciclo excéntrico que no termine en 4,2,1. ¿Qué implicaciones matemáticas tendrían la existencia de esos números? Recordemos que la función 5n+1 sí muestra números que divergen hasta el infinito; por otra parte, la conjetura de Poyla parecía ser válida desde que fue enunciada en 1919 y no fue sino hasta 1958 que se encontró un contraejemplo que mostró su falsedad. Pero la conjetura de Collatz parece ser mucho más escurridiza.
Podemos encontrar más patrones si a este árbol le asignamos un cierto grado de inclinación diferente a los números pares o impares, el resultado es un asombroso patrón fractal que crece a medida que añadimos más números, y que asemeja al crecimiento orgánico de algas y corales. ¡Infinitos filamentos y ramas ocultos en una simple operación!
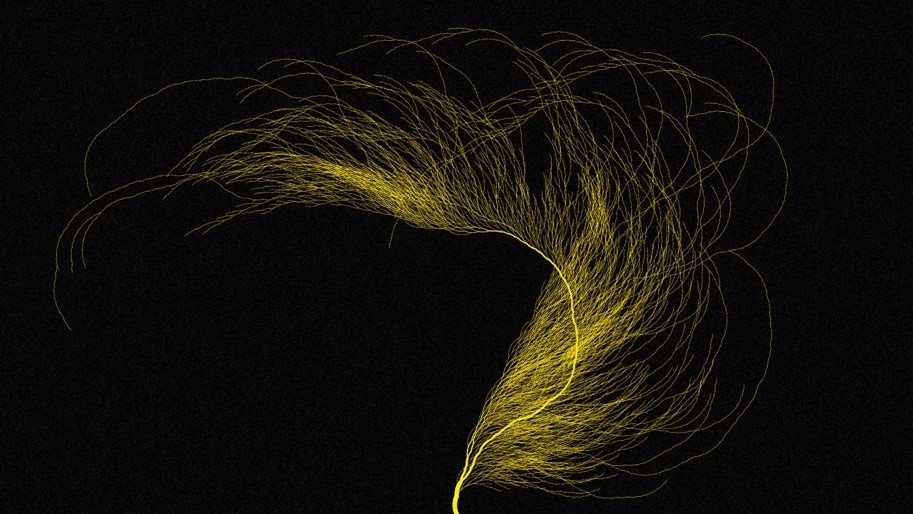
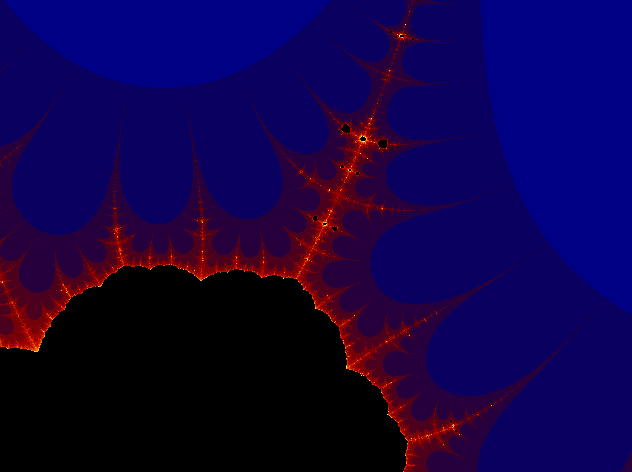
Desde un punto de vista matemático los fractales se generan por un proceso de iteración, es decir, por la repetición continua de la misma operación a los resultados, una y otra vez; justo el tipo de operaciones implícitas en la conjetura de Collatz. Uno de los fractales más asombrosos y conocidos es el fractal de Mandelbrot. Es una imagen autosimilar (como todo fractal) cuya peculiaridad está en que no es un fractal lineal -que repita simplemente la misma estructura- sino que además de repetir la estructura principal, incluye infinitos patrones en diferentes niveles. Hemos explicado en otros artículos que este tipo de fractales constituyen una expresión gráfica de la ley dialéctica de la “negación de la negación”-además de la unidad de contrarios que implica lo finito e infinito- que, en pocas palabras, establece que en todo proceso las etapas que la componen niegan a las anteriores, las superan, pero conservándolas al mismo tiempo. Un fractal parecido al de Mandelbrot aparece en la conjetura de Collatz si, bajo ciertas condiciones, la graficamos en el plano complejo -es decir, incluyendo números complejos-: “Es decir, calculamos la órbita de cada número complejo bajo la función y representamos de negro los puntos cuya órbita sea convergente. Nos queda la siguiente representación, denominada fractal de Collatz:”[17] Asignando colores y observando a escala, nos encontramos con un universo infinito:
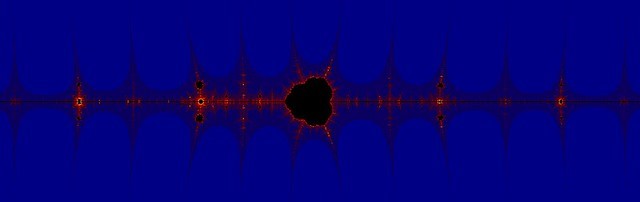
“Pero, ¿es un fractal en el sentido del conjunto de Mandelbrot? Pues eso parece. Analizando la imagen anterior vemos que tiene ciertas similitudes al fractal de Mandelbrot, pero además si hacemos zoom en varias partes (principalmente en las cercanas al borde del conjunto) encontraremos autosimilitud como se encuentra en el conjunto. Por ejemplo, aquí tenemos una imagen después de hacer zoom cerca del borde del conjunto central” “este fractal de Collatz, como la mayoría de los fractales de su tipo, es un mundo donde a cada paso nos encontramos con algo nuevo a la vez que conocido”.
Una metáfora dialéctica del universo
Los fractales no lineales son una expresión gráfica de la infinita complejidad del universo mismo. Hablamos de un conjunto que contiene infinitos patrones a diferentes niveles, cada uno de los cuales es nuevo pero contiene y repite, de cierta forma, patrones de niveles aparentemente dejados atrás; en lo micro aparecen patrones que existen en la totalidad y a la inversa. El universo parece ser así: super cúmulos de galaxias, galaxias, sistemas planetarios, planetas, continentes, cuerpos diversos, moléculas, átomos, partículas subatómicas… cada nivel tiene sus propios patrones y leyes pero, de cierta forma, los elementos -por poner un ejemplo- parecen repetir la estructura de un sistema planetario y ser inagotables en sí mismos, pues hasta la fecha cada partícula supuestamente elemental ha demostrado descomponerse en otras partículas más evanescentes, en un proceso sin fin a la vista. El universo en sí mismo se ha mostrado, sucesivamente, como un conjunto infinito, inagotable y profundamente dialéctico.
En conclusión, la conjetura de Collatz esconde asombrosos patrones dialécticos. Su comportamiento es un ejemplo más de la forma concreta y determinada en que se manifiestan las leyes más generales del materialismo dialéctico en diversos campos, en este caso, las matemáticas. Así mismo, como sostuvo Hegel, la primera ley de la dialéctica es que la verdad es siempre concreta o una síntesis de múltiples determinaciones: el movimiento dialéctico se manifiesta de forma concreta en diferentes niveles en que existe la realidad: la naturaleza, la sociedad y el pensamiento. No basta con enunciar las tres leyes de la dialéctica a la manera de los viejos manuales soviéticos -que convirtieron al materialismo dialéctico en una serie de ideas abstractas sin vida- sino mostrar esas leyes en sus manifestaciones concretas y a partir del avance de la ciencia misma, de tal forma que el pensamiento dialéctico se demuestre como un instrumento necesario para interpretar la realidad e intervenir en ella .





